新加坡科廷大学本科课程和作业辅导机构

　　Hello~大家好，可能同学们也发现了，由于国内外教育方式的不同，很多课程上的知识点无法自己梳理清楚，笔记也记录的不是特别全面。今天学姐为同学们分享数学专业相关理论，希望可以帮助广大留学生梳理思路，学姐整理了非常详细的流程细节可以参考。

　　主要学习目标

　　1、确定微分方程的阶。

　　2、解释微分方程的解是什么意思。

　　3、区分微分方程的通解和特解。

　　4、确定一个初始值问题。

　　5、确定给定的函数是微分方程的解还是初值问题。

　　微积分是变化的数学，变化率用导数表示。因此，使用微积分最常见的方法之一是建立一个包含未知函数的方程 y=f(x) 及其导数，称为微分方程。求解这样的方程通常提供关于量如何变化的信息，并且经常提供关于变化如何以及为什么发生的洞察。

　　求解微分方程的技术可以采取许多不同的形式，包括直接求解、使用图形或计算机计算。我们在本章中介绍了主要思想，并在课程的后面更详细地描述了它们。在本节中，我们研究什么是微分方程，如何验证它们的解，一些用于求解它们的方法，以及一些常见和有用的方程的例子。

　　一般微分方程

　　考虑一下等式 y'=3x2, 这是一个微分方程的例子，因为它包含一个导数。变量之间是有关系的 x 和 y:y 是的未知函数 x 。此外，方程的左手边是 y 。因此我们可以这样解释这个方程:从某个函数开始 y=f(x) 取它的导数。答案必须等于 3x2 。什么函数的导数等于 3x2 ?其中一个功能是 y=x3 ，所以这个函数被认为是解决办法微分方程。

　　一般和特殊解决方案

　　我们已经注意到微分方程 y'=2x 至少有两种解决方案: y=x2 和 y=x2+4 。这两个解唯一的区别就是最后一项，是常数。如果最后一项是不同的常数呢?这个表达式还会是微分方程的解吗?事实上，任何形式的功能 y=x2+C ，哪里 C 代表任何常数，也是一种解决方案。原因是，的导数 x2+C 存在 2x ，不考虑的值 C 。可以看出，这个微分方程的任何解都必须是 y=x2+C 。这是一个通解微分方程。这些解决方案的图表如图所示 8.1.1 。(注意:在这个图中，我们使用了介于之间的偶数整数值 −4 和 4 。事实上，对的价值没有限制 C ;它可以是整数，也可以不是。)

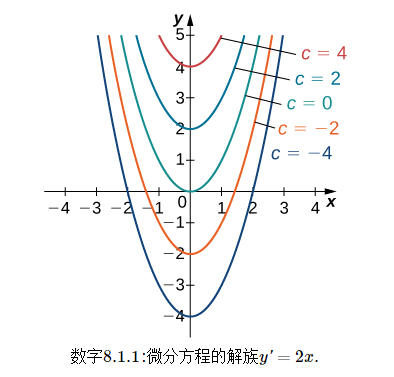
　　在这个例子中，我们可以自由选择任何我们希望的解决方案;例如， y=x2−3 是这个微分方程解族的一员。这叫做微分方程的特殊解。如果给我们关于问题的额外信息，一个特定的解决方案通常可以被唯一地识别。

　　考而思新加坡大学课程的在线辅导可以添加考而思老师微信进行一对一咨询，在新加坡大学留学的同学们如果遇到困难了可以直接联系我们。考而思专注辅导海外留学生在学习中遇到的各种困难。